FUNCIÓN LOGARÍTMICA

Una ecuación logarítmica es aquella en la que la incógnita se encuentra en el argumento de logaritmos. Su resolución se reduce, en realidad, a la resolución de ecuaciones del mismo tipo que las expresiones de los argumentos (ecuaciones de segundo grado, tercer grado, irracionales...)
$$lo{g}_b\left(a\right)=c\iff b^c=a$$

• a es la base del logaritmo
  
• b es el argumento del logaritmo
  
• c es el número tal que
  
  $$b^c=a$$

Por tanto, c es el exponente al que tenemos que elevar la base b para obtener el número a.

$$b^{lo{g}_b\left(c\right)}=c$$

• Si b es el número e, escribimos ln(x) en lugar de log_e (x). Es el logaritmo Neperiano.

Propiedades de los logaritmos

logaritmo del producto:

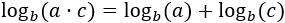logaritmo del cociente:

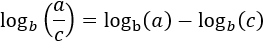logaritmo de la potencia:

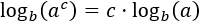cambio de base:

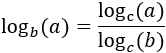Propiedad útil en la práctica:

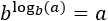Ejercicios:

Ecuación 1

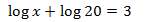
Ver Solución

Usaremos las propiedades de los logaritmos y que
$$log\left(1000\right)=log\left({10}^3\right)=3$$

Tenemos una igualdad entre logaritmos, entonces los argumentos (lo de dentro) tienen que ser los mismos

La solución es x = 50.


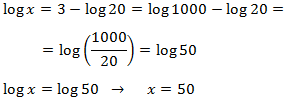
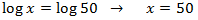
Ecuación 2

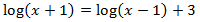
Ver Solución

Usaremos la propiedad del logaritmo del cociente y escribimos 3 como
$$3=log\left({10}^3\right)=log\left(1000\right)$$

para conseguir una igualdad de logaritmos

Los logaritmos son iguales cuando sus argumentos (lo de dentro) son los mismos. Es decir, queremos

Resolvemos la ecuación

Ahora tenemos que comprobar que para la solución obtenida los argumentos son positivos (para que existan los logaritmos).
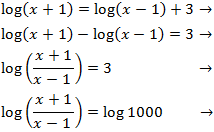
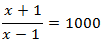
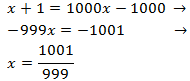
$$x+1=\frac{1001}{99}>0$$ $$x-1=\frac{1001}{99}-1\simeq 0.002>0$$ Por tanto, es la solución.