x2+y2=r2
Si la circunferencia no está centrada en el (0,0)
, es posible armar un nuevo sistema de modo tal que el centro de la circunferencia coincida con el nuevo origen de coordenadas. Por ejemplo consideremos:
(x–α)2+(y–β)2=r2
Si hacemos un cambio de variables:
{x′=x–αy′=y–β
En las nuevas variables la ecuación queda expresada en forma canónica:
x′2+y′2=r2
Para obtener la ecuación canónica, hicimos una traslación de ejes, de modo que el centro del nuevo sistema coincidiera con el centro de la circunferencia:
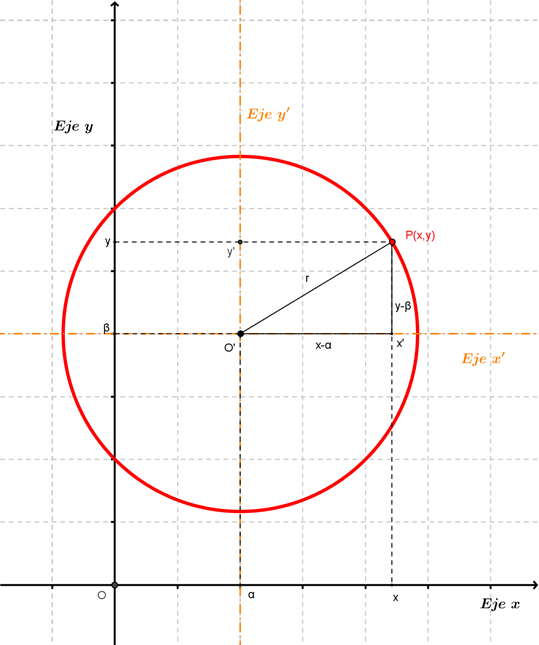
Ejemplo
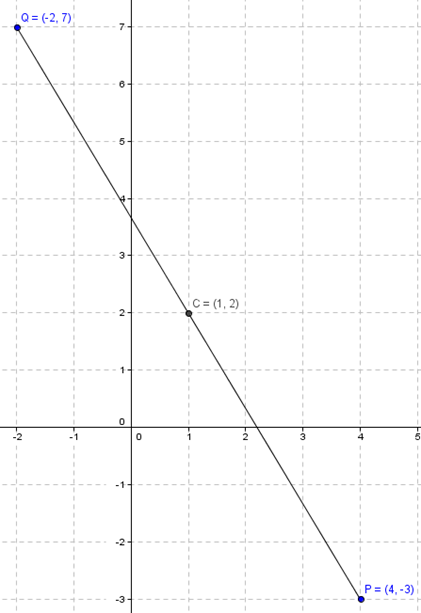
Encuentre la ecuación de una circunferencia si los extremos de uno de sus diámetros son P(4,–3)y Q(–2,7).
Conociendo los extremos de un diámetro, ¿cómo obtendrían el centro? ¿Y el radio?
Resolución
Como el segmento PQes un diámetro, el centro es el punto medio de este segmento. Y el radio es la mitad de la distancia entre PyQ:
−−→PQ=(–6,10)⇒−−→PQ=2√34
radio=√34
Entonces ya tenemos las coordenadas del centro, y tenemos el radio. Basta con reemplazar en la ecuación ordinaria para obtener la ecuación de esta circunferencia:
(x–1)2+(y–2)2=34
La gráfica es:
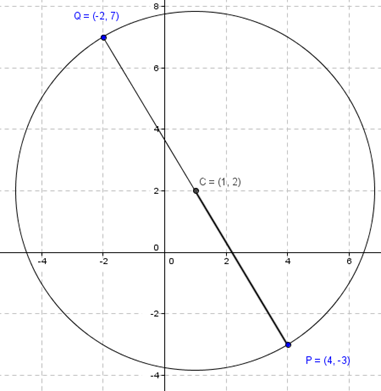
No hay comentarios:
Publicar un comentario