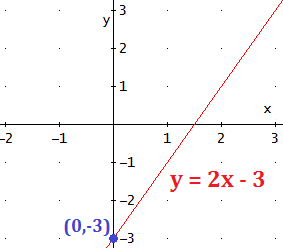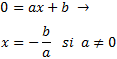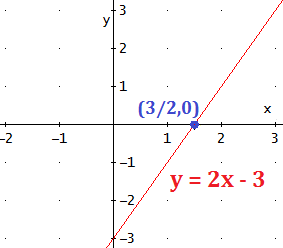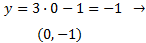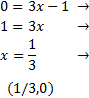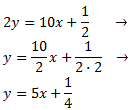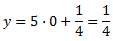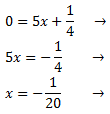Operación entre Conjuntos

Ejercicio

Se encuestó a 100 personas sobre sus preferencias en relación a dos programas (no excluyentes) municipales contra la delincuencia. Los programas recibieron los nombres A y B.

Los resultados fueron los siguientes:

• 65 no prefieren el programa  A
• 45 no prefieren el programa  B
• 50 prefieren los programas A o B, pero no ambos

Se pide determinar el número de encuestados que prefieren ambos programas.
Sol: Usamos el siguiente Diagrama de Venn

 

CIRCUNFERENCIA

Hay un caso particular de circunferencia, que tiene su centro en el origen. La ecuación que la define se llama ecuación canónica de la circunferencia:
$$x^2+y^2=r^2$$
Si la circunferencia no está centrada en el $\left(0,0\right)$
, es posible armar un nuevo sistema de modo tal que el centro de la circunferencia coincida con el nuevo origen de coordenadas. Por ejemplo consideremos:
$${\left(x–\alpha \right)}^2+{\left(y–\beta \right)}^2=r^2$$
Si hacemos un cambio de variables:
$$\{\begin{array}{c}{x}^{\prime }=x–\alpha \\ y^{\prime }=y–\beta \end{array}$$
En las nuevas variables la ecuación queda expresada en forma canónica:
$$x^{\prime 2}+y^{\prime 2}=r^2$$
Para obtener la ecuación canónica, hicimos una traslación de ejes, de modo que el centro del nuevo sistema coincidiera con el centro de la circunferencia:

Ejemplo

Encuentre la ecuación de una circunferencia si los extremos de uno de sus diámetros son $P\left(4,–3\right)$
y $Q\left(–2,7\right)$.
Conociendo los extremos de un diámetro, ¿cómo obtendrían el centro? ¿Y el radio?

Resolución

Como el segmento $PQ$
es un diámetro, el centro es el punto medio de este segmento. Y el radio es la mitad de la distancia entre $PyQ$:

$$C=\left(\frac{4+\left(–2\right)}{2},\frac{–3+7}{2}\right)=\left(1,2\right)$$
$$\overrightarrow{PQ}=\left(–6,10\right)\Rightarrow \overrightarrow{PQ}=2\sqrt{34}$$
$$radio=\sqrt{34}$$
Entonces ya tenemos las coordenadas del centro, y tenemos el radio. Basta con reemplazar en la ecuación ordinaria para obtener la ecuación de esta circunferencia:
$${\left(x–1\right)}^2+{\left(y–2\right)}^2=34$$
La gráfica es:

ELIPSE

 

Una elipse es el conjunto de todos los puntos de un plano cuya suma de distancias a dos puntos fijos es una constante. Así que, no importa dónde estés en la elipse, puedes sumar las distancias al punto "A" y al punto "B" y siempre saldrá lo mismo. (Los puntos "A" y "B" se llaman los focos de la elipse)

 Ejercicios:

1 )   Calcular los ejes, focos, excentricidad y representar gráficamente cada una de las siguientes elipses:

PUNTOS Y RECTAS

La ecuación de una recta es de la forma

$$y=ax+b$$

Ejemplo:

Al número a se le llama pendiente y a al número b, término independiente u ordenada al origen.

---

Puntos de corte de una Recta

Puntos de corte o intersección con los ejes:

Con el eje OY (de ordenadas)
Ocurre cuando x = 0. Sustituimos x por 0 en la ecuación y obtenemos el valor de y. Es decir, y = b. El punto es (0, b).
Ejemplo:

Con el eje OX (de abscisas):
Ocurre cuando y = 0. Sustituimos y por 0 en la ecuación y calculamos x. Es decir,

El punto es (-b/a,0).
Ejemplos:

 

Problemas

Calcular los puntos de corte de los ejes con la rectasiguiente. ¿Cuál es la pendiente de la recta?

 

Solución:

La pendiente es el coeficiente de la x, es decir, 3.
Como la pendiente es positiva, la recta será creciente.
Puntos de corte con el eje OY: ocurre cuando x = 0. Sustituimos en la ecuación:

Con el eje OX: ocurre cuando y = 0. Sustituimos en la ecuación:

La gráfica es

* Calcular los puntos de corte de los ejes con de la recta. ¿Cuál es la pendiente de la recta

 

Solución

Escribimos la ecuación en su forma general:

Por tanto, la pendiente es 5. Como es positiva, la recta es creciente.

Cortes con el eje OY: ocurre cuando x = 0. Sustituimos en la ecuación:

El punto es (0,1/4).

Con el eje OX: cuando y=0. Sustituimos en la ecuación:

El punto es (-1/20,0)

La gráfica de la recta es

 

---

PARÁBOLA

La ecuación general de una parábola es

$$y=a{x}^2+bx+c$$

los coeficientes b y c pueden ser 0. Si a = 0, es una recta y no una parábola.

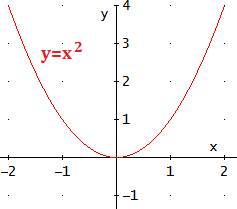
• Cuando a > 0, la parábola tiene forma de U.
  
  
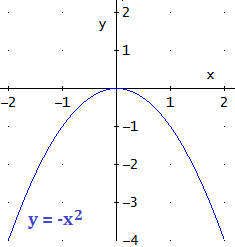
• Cuando a < 0, tiene forma de U invertida.
  
  

---

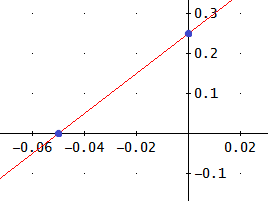
Puntos de corte

Con el eje OY (de ordenadas):
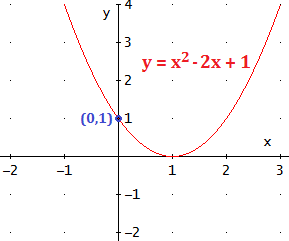
Ocurre cuando x = 0. Es decir, y = c. El punto es (0,c).
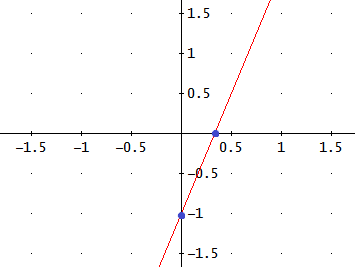
Ejemplo:

Con el eje OX (de abscisas):
Ocurre cuando y = 0. Es decir,

$$0=a{x}^2+bx+c$$

Tenemos una ecuación de segundo grado. Por tanto, puede haber 1, 2 o ningún punto de corte.
Ejemplos:
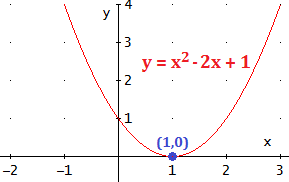
La parábola y = x² - 2x + 1 tiene sólo un punto de corte con el eje de abscisas ya que la ecuación sólo tiene una solución:

$$x=\frac{2\pm \sqrt{4-4}}{2}=\frac{2\pm 0}{2}=1$$

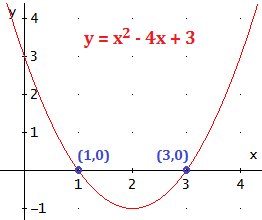
La parábola y = x² - 4x + 3 tiene dos puntos de corte con el eje de abscisas ya que la ecuación tiene dos soluciones:

$$x=\frac{4\pm \sqrt{16-12}}{2}=\frac{4\pm 2}{2}=3,1$$

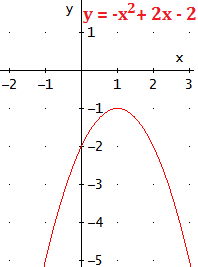
La parábola y = - x² + 2x - 2 no tiene puntos de corte con el eje de abscisas ya que la ecuación no tiene soluciones (reales):

$$x=\frac{-2\pm \sqrt{4-8}}{-2}=\frac{-2\pm \sqrt{-4}}{-2}$$

PERÍMETRO Y AREA

Perímetro: es la suma de los lados de una figura geométrica. Es su contorno.
Área: es la medida de la superficie de una figura; es decir, la medida de su región interior.

Ejercicios  


1.- Un triángulo cuya base mide 10 cm, su lado 43.17 cm y su altura 42 cm


2.- Una mesa cuadrada de 1.20 m de lado.

3.- Una superficie cuadrada cuya diagonal mide 8 cm.

Al conocer su área puedo obtener la medida de su lado al extraer raíz cuadrada a 32 que es 5.6568542495


4.- Un rombo cuyas diagonales miden 5.4 cm y 3cm.
Con los datos conocidos puedo obtener el área.

Para saber la medida de su lado utilizo el Teorema de Pitágoras y así poder obtener el perímetro. Aproximadamente el lado mide 3.088 cm


5.- Una tapa de zapatos que mide 38 cm de largo por 21 cm de ancho.


6.- Un trapecio cuyas bases miden 12 y 15 cm y de altura mide 6 cm

Al trazar el trapecio con las medidas conocidas, puedo saber la medida de su lado utilizando el Teorema de Pitágoras para obtener el  perímetro.


7.- Un pentágono regular que mide 7.265 cm de lado y 5 cm de apotema.

8.- Un hexágono regular de 3.46 cm de lado y 3 cm de apotema.


9.- Un círculo cuyo diámetro mide 6 cm